
Going back to the Method 1 example where we were calculating the standard deviation for cells C2 to C11, you should write C2:C11.
Next, in the Function Arguments window, enter the range for which you want to calculate the standard deviation into the text box next to Number1.Then, select Statistical, browse the list below and select either STDEV.P or STDEV.S.Now, click the arrow next to Or select a category to open the dropdown menu.After that, click the Insert Function button.Here, the numbers are present in cells from A2 to A11, so we type STDEV.S(A2:A11) in the formula bar. Type the formula STDEV.S( and select the data range containing the values for which standard deviation is sought. Next, click the Formulas header in the Main Menu. Go to the cell where you want to display the standard deviation.

Click on the cell where the deviation result will appear.
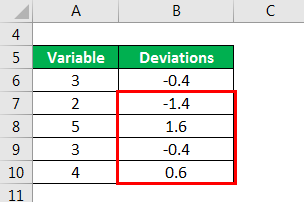
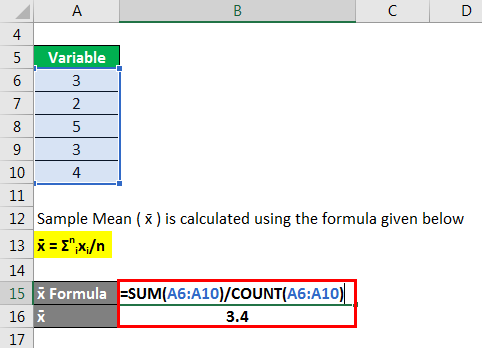
Let’s see how to get the deviations without typing the formulas. In the uncorrelated errors case, we have Vdar bjX n X0X 1 e2 i i1 x x i 0 X0X 1 X n 0X n 1 1 n e2 n i i1 x x i 0 X0X n 1 1 E 1 n x ix 0 1 n e2 x E 1 ix 0 0 n x ix i1 and for the general Newey-West standard. It is great when you’re in a crunch but don’t want to mess with the formulas. We can also write these standard errors to resemble the general GMM standard errors (see page 23 of Lecture 8). The next method is almost as fast as the first one and doesn’t require in-depth Excel knowledge.
Click the arrow next to General to open the dropdown menu. The accuracy of a sample that represents a population is known through this formula. If you want to round the result to two decimals, select the results and click on the Home tab. The standard error is an important statistical measure and it is related to the standard deviation. In this example, you want to calculate STDEV.P for cells C2 to C11 and STDEV.S for cells C4 to C7. The values in the brackets denote the range of cells for which you want to calculate the standard deviation value. Click on the cell where you’d like the standard deviation value to be displayed. 3.1 Standard error of mean versus standard deviation. 2 Student approximation when σ value is unknown. 1.4 Independent and identically distributed random variables with random sample size. In regression analysis, the term "standard error" refers either to the square root of the reduced chi-squared statistic, or the standard error for a particular regression coefficient (as used in, say, confidence intervals). In other words, the standard error of the mean is a measure of the dispersion of sample means around the population mean. Therefore, the relationship between the standard error of the mean and the standard deviation is such that, for a given sample size, the standard error of the mean equals the standard deviation divided by the square root of the sample size. This is because as the sample size increases, sample means cluster more closely around the population mean. Mathematically, the variance of the sampling distribution obtained is equal to the variance of the population divided by the sample size. This forms a distribution of different means, and this distribution has its own mean and variance. The sampling distribution of a mean is generated by repeated sampling from the same population and recording of the sample means obtained. If the statistic is the sample mean, it is called the standard error of the mean ( SEM). The standard error ( SE) of a statistic (usually an estimate of a parameter) is the standard deviation of its sampling distribution or an estimate of that standard deviation. For a value that is sampled with an unbiased normally distributed error, the above depicts the proportion of samples that would fall between 0, 1, 2, and 3 standard deviations above and below the actual value.







 0 kommentar(er)
0 kommentar(er)
